无论你是在寻找最佳的应聘者还是最合适的配偶，找到那个“对”的人，从来都不是件容易的事，因为你不知道其余的人是怎样的，或者相比于你已经见到的人是怎样的。

幸运的是，一个叫“寻找最优解”（optimal-stopping theory）的数学理论可以帮助你找到最适合的那个人。

就职于伦敦大学学院高级空间分析中心的数学家汉娜·福瑞（Hannah Fry）在她的2014TED演讲中解释了这个理论。最近她还出版了一本书叫做《爱的数学》。这个理论本质上就是帮助你知道什么时候该停止寻找并做出正确决定。《华盛顿邮报》对该书和作者的演讲给予了肯定：“这是通向浪漫的机智指南……不论是演讲还是书里，福瑞都向人们深刻但易懂地阐述了一些由来已久的问题。”

她在演讲中举了一个寻找配偶的例子。在这个例子中，你会花一些时间谈很多个朋友并逐渐加强对谈恋爱的理解，你会拒绝前37%的追求者并与接下来的一个比以前所有人都出色的人结婚。

按照这个逻辑，如果你打算一生中与10个人约会，你就需要拒绝前四个人，如果你打算与20个人约会，你就需要拒绝前8个人。

但是一般人们不会计划说与多少人约会，所以这个方法可以应用到实践上。比如你如果现在15岁并想在35岁的时候结婚，这时你就要拒绝前37%的时间段中你所遇到的所有人，也就是22岁之前，然后与你22岁之后遇到的比之前所有人都要出色的人结婚。

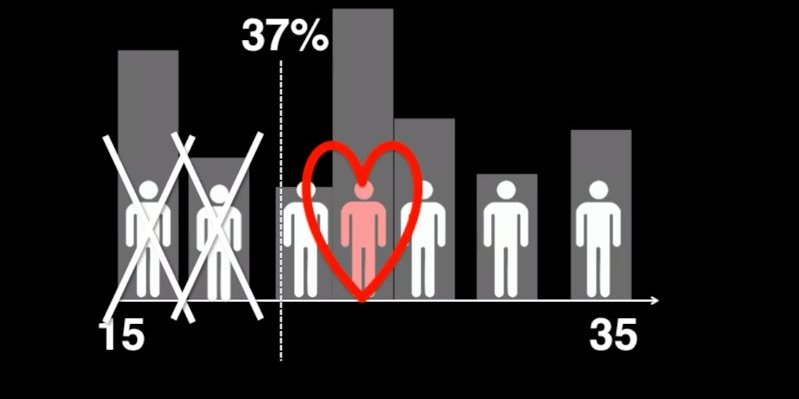
如果你不按这个策略，而只是在你大约会与之约会的20个约会者中随机选一人结婚，那你找到真爱的几率只有5%，而如果你照着这个策略做了，你找到最佳配偶的几率将提升到38.4%。

同样的逻辑可以应用到招聘中。实际上“秘书的难题”是这个理论最有名的例子。就是说，如果你想招聘一个新助手并对应聘者进行面试，你永远不能知道你没有面试的人中是否有比之前面试过的都优秀的人，但是你不可能永远的面试下去，所以你必须在合适的时机停止面试并做出决定。

按照寻找最优解的策略，你最佳的决定就是拒绝前37%的应聘者并雇佣接下来面试的一个比之前所有人都出色的人。同样你也可以以时间来度量，如果你计划用三个月的时间来招聘，那么你应该拒绝第一个月的所有应聘者并雇佣后面一个比之前所有人都出色的应聘者。

当然这个策略不是没有风险的，你有可能在前期遇到最合适的那个人并在之后再也没有遇到更合适的人；或者是你运气不好，在前期遇到的都是些奇葩，然后在接下来选了一个稍微正常点的但不是最好的人选。

但是福瑞说了，“有足够的耐心等到真爱和在合适的时机做出决定以免好的都被挑走，这两者之间是一场奇妙的博弈。即使考虑到所有的风险，这个理论仍然值得付诸实践。”

下面是福瑞在TED的演讲：

终于相信数学家可以拯救世界了吧？